数据结构-树

# 前置定义

满(full)二叉树：
- 英文wiki：每个节点都有0或2个子节点
- 国内教材：除最低层的节点外，每个节点都有2个子节点（即第 $i$ 层的节点数为 $2^i-1$ ）
完美(perfect)二叉树：（国内版）满二叉树
完全二叉树：除最底层外，每一层都被填满；最底层的节点尽可能靠左。

In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible

# AVL树

定义：

AVL树：高度平衡的二叉搜索树（任意节点的两个子树的高度差 $\le$ 1）
平衡因子：某个节点的右子树高度-左子树高度

因此，AVL树又可作如下定义：任意节点平衡因子的绝对值小于等于1的二叉搜索树

当插入或删除节点导致不平衡时，AVL通过旋转节点来重新平衡节点。

# 旋转时发生了什么

如图，设根节点的左子节点高度为 $h_l$ ，右子节点高度为 $h_r$ ，下面以右旋为例

右旋以后，左子节点的高度为 $h'_l$ ，右子节点高度为 $h'_r$ ，观察可知

$\begin{aligned}h'_l&\le h_l - 1\\ h'_r&\le max(h_r+1,h_l)\end{aligned}$

显然右旋时，需要根据 $h_e$ 来进行分类讨论。

# 插入/删除操作

同样以右旋为例

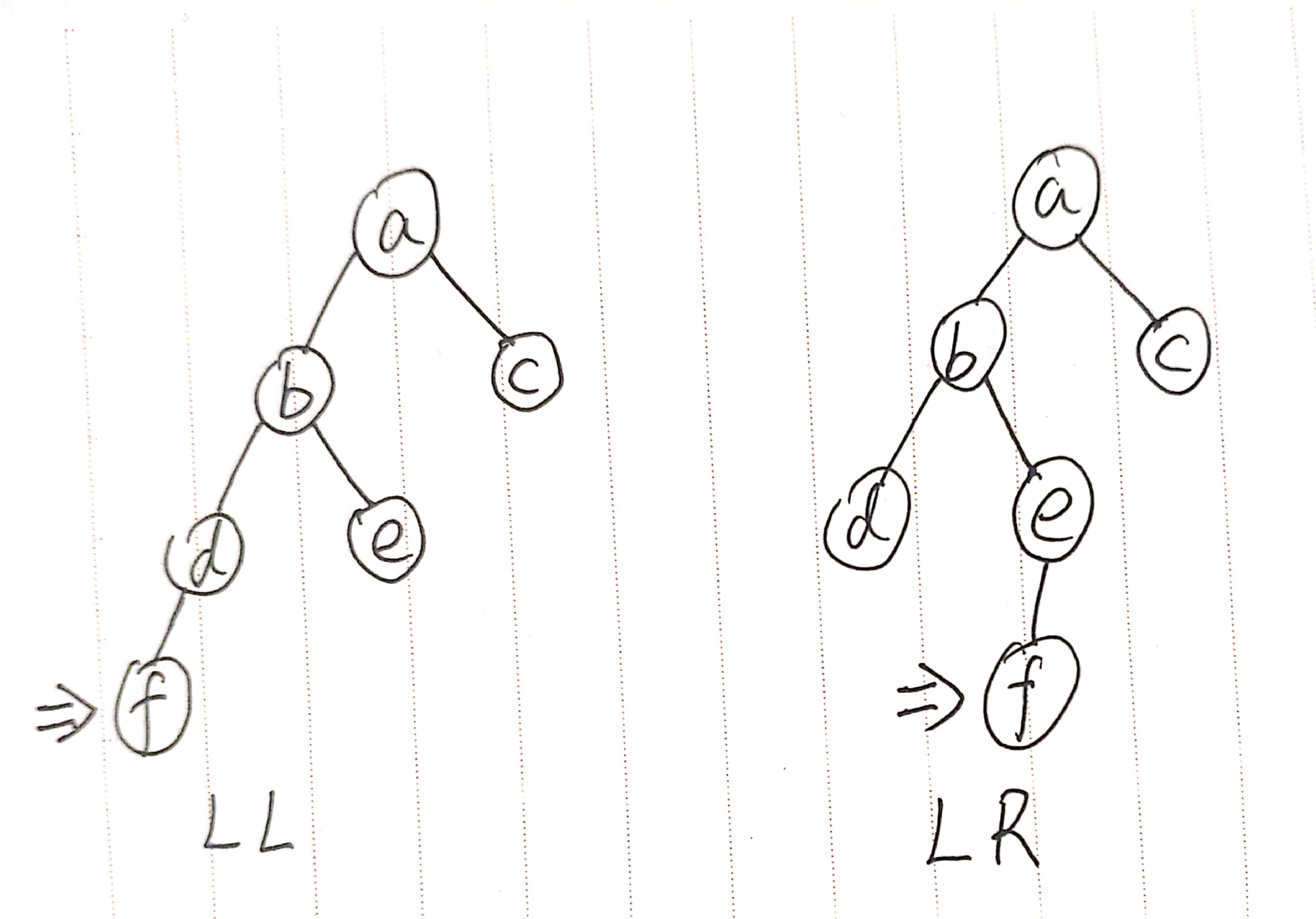
# LL型

假设插入 $f$ 后使得当前子树 $a$ 失衡，且 $h_b=h_d+1$

由于插入前是AVL树，因此 $h_e\le h_c$

对 $b$ 进行一次右旋，新的树有 $h'_l=h_l-1,h'_r=max(h_e,h_c)+1=h_c+1$

删除操作同理

# LR型

假设插入 $f$ 后使得当前子树 $a$ 失衡，且 $h_b=h_e+1$

如果直接右旋，会导致 $h'_r=h_e+1>h_r$

因此要先对 $e$ 进行一次左旋，再对 $e$ 进行右旋

删除操作同理

# Java实现及测试代码

实现了插入、删除操作

关键字不可重复

package DataStructure.Tree;

import com.sun.istack.internal.Nullable;

import java.util.ArrayList;
import java.util.List;

public class AVLTree<T extends Comparable<T>> implements Tree<T>{

    private AVLNode<T> root;

    @Override
    public void insert(T value) {
        root = insert(value, root, null);
    }

    @Override
    public void remove(T value) {
        root = remove(value, root);
    }

    @Override
    public List<T> travel() {
        ArrayList<T> result = new ArrayList<>();
        travel(result, root);
        return result;
    }

    private AVLNode<T> insert(T value, AVLNode<T> node, AVLNode<T> parent){
        if(node == null) return new AVLNode<>(value, null, null, parent);
        if(node.value.compareTo(value) == 0) return node;

        int dir = node.value.compareTo(value) > 0 ? 0: 1;
        node.children[dir] = insert(value, node.children[dir], node);
        node.updateHeight();
        return rebalance(node);
    }

    private AVLNode<T> remove(T value, AVLNode<T> node){
        if(node == null) return null;
        if(node.value.compareTo(value) == 0){
            // 没有子节点
            if(node.children[0] == null && node.children[1] == null) return null;

            // 只有一个子节点
            if(node.children[0] == null || node.children[1] == null){
                int notNullIdx = node.children[0] == null ? 1 : 0; // 子节点方向
                node.children[notNullIdx].parent = node.parent;
                return node.children[notNullIdx];
            }

            // 有两个子节点，先按常规BST的方法删除
            AVLNode<T> least = node.children[1];
            while(least.children[0] != null) least = least.children[0];
            node.value = least.value;
            least.parent.children[getDirection(least)] = least.children[1];
            if(least.children[1] != null) least.children[1].parent = least.parent;
            least.parent.updateHeight();
            // 从least节点开始，一直向上rebalance
            AVLNode<T> current = least.parent;
            while(current != node){
                current.updateHeight();
                current = rebalance(current).parent;
            }
            return rebalance(node);

        } else {
            int dir = node.value.compareTo(value) > 0 ? 0 : 1;
            node.children[dir] = remove(value, node.children[dir]);
            node.updateHeight();
            return rebalance(node);
        }
    }

    /**
     * 对节点进行再平衡
     */
    private AVLNode<T> rebalance(AVLNode<T> node){
        // dir: 重子树（高度更高的子树）的位置
        int dir = height(node.children[0]) > height(node.children[1]) ? 0 : 1;
        int heavy = height(node.children[dir]);
        int light = height(node.children[dir ^ 1]);
        if(Math.abs(heavy - light) >= 2){
            if(height(node.children[dir].children[dir]) > height(node.children[dir].children[dir ^ 1])){
                return rotate(node.children[dir]); // LL 或 RR
            }else{ // LR 或 RL
                AVLNode<T> n = node.children[dir].children[dir ^ 1];
                return rotate(rotate(n));
            }
        }
        return node;
    }

    /**
     * 将节点左旋（或右旋）
     */
    private AVLNode<T> rotate(AVLNode<T> node){
        if(node == root) throw new IllegalStateException("不能旋转根节点");

        AVLNode<T> parent = node.parent;
        AVLNode<T> grandParent = parent == null ? null : parent.parent;
        int direction = getDirection(node);

        node.parent = grandParent;
        if(grandParent != null) grandParent.children[getDirection(parent)] = node;
        parent.children[direction] = node.children[direction ^ 1];
        if(node.children[direction ^ 1] != null) parent.children[direction].parent = parent;
        node.children[direction ^ 1] = parent;
        parent.parent = node;

        parent.updateHeight();
        node.updateHeight();

        if(node.parent == null) root = node;
        return node;
    }

    /**
     * 获取当前节点对于父节点的方向
     * @return 如果当前节点为父节点的左子节点，则返回0，否则返回1
     */
    private int getDirection(AVLNode<T> node){
        if(node.parent == null) throw new IllegalStateException("不能对根节点调用getDir");
        return node.parent.children[0] == node ? 0 : 1;
    }

    /**
     * 中序遍历二叉树
     */
    private void travel(List<T> result, AVLNode<T> node){
        if(node != null){
            travel(result, node.children[0]);
            result.add(node.value);
            travel(result, node.children[1]);
        }
    }

    public static int height(AVLNode<?> node){
        return node == null ? 0 : node.height;
    }

    private static class AVLNode<T> {
        private int height = 1;
        private AVLNode<T>  parent;
        private AVLNode<T>[] children = new AVLNode[2];
        private T value;

        private AVLNode(T v, @Nullable AVLNode<T> left, @Nullable AVLNode<T> right, @Nullable AVLNode<T> parent){
            value = v;
            children[0] = left;
            children[1] = right;
            this.parent = parent;
            updateHeight();
        }

        private void updateHeight(){
            height = Math.max(height(children[0]), height(children[1])) + 1;
        }
    }

}

# 优化

插入优化：

在插入单个一个新节点时，从被插入的节点 $i$ 到树的根节点 $root$ 这一路径上所有节点的 $BF$ (平衡因子)都可能会被改变，因此需要回溯更新。

但如果某一节点 $j$ 的 $BF$ 更新后为 $0$ ，则说明以 $j$ 为根的这一子树高度没有发生变化，因此 $j$ 到 $root$ 这些节点不需要再更新。
删除优化：

再删除一个节点以后，从被删除的节点 $i$ 到根节点 $root$ 路径上的 $BF$ 都可能改变，因此要回溯更新。

由于删除单个节点，子树的高度最多减1；如果某一节点 $j$ 的 $BF$ 从 $0$ 变为了 $1/-1$ ，那么说明 $j$ 的高度没有变化，因此后续节点不需要再回溯更新。

# 参考资料

https://en.wikipedia.org/wiki/AVL_tree

# B树（B-树）

B树是一种自平衡多叉树。

性质：对于一个 $m$ 阶B树：

所有叶子节点在同一层
每个节点至多有 $m$ 个子树
除根/叶子节点外，每个节点至少有 $\lceil \frac{m}{2}\rceil$ 个子树，所有节点的子树个数（即出度数）= 关键码个数 + 1
根节点至少有两个子树

也就是说，根节点的关键字数量 $k$ 满足 $1\le k \le m-1$ ，非根节点关键字数量 $k'$ 满足 $\lceil \frac{m}{2}\rceil - 1 \le k' \le m-1$

$M$ 阶B树也被称为 ( $\lceil \frac{m}{2}\rceil$ , $m$ )树。如 $M=3$ ，则称为2-3树

# 插入与删除

# 插入

插入时总是插入到叶子节点中。当节点的关键字个数超过 $m-1$ 时，需要进行调整。

下图是一个3-5树，此时坐下的节点不符合B树性质，需要进行分裂

取 $(18,22,23,25,39)$ 中间的值（即23），将其放入父节点中，并将原节点分裂成两部分

若分裂后父节点的关键字个数大于4，则需要进一步分裂父节点。

# 删除

删除时需要考虑的情况较多，记 $mn$ 为非根节点关键字个数下限，即 $mn=\lceil \frac{m}{2}\rceil - 1$

删除的是叶子节点中的关键字
- 删除后未破坏B树性质：无需处理
- 删除后破坏B树性质（关键字个数小于 $mn$ ）：
  - 如果兄弟节点（左侧或右侧的任意一个）的关键字个数大于 $mn$ ：
    
    先将父节点的一个关键字移动到当前节点（前驱或后继）
    
    然后，从兄弟节点中取一个关键字移动到父节点中，删除操作完成
  - 如果兄弟节点的关键字个数等于 $mn$ ：
    
    先将父节点的一个关键字移动到当前节点
    
    由于 $2\times(\lceil \frac{m}{2}\rceil - 1)\le m-1$ ，因此可以将当前节点与兄弟节点合并
    
    若此时父节点关键字个数不满足B树性质，则需要继续向上修正
需要特别说明的是：
1. 如果能够从兄弟节点借，此后父节点必定满足B树性质，无需继续向上修正
2. 因此，若对非叶子节点进行修正，则之前执行的必定是合并操作
删除的是非叶子结点中的关键字 $r$

此时需要将关键字 $r$ 替换为后继 $k$ （或前驱），并在子节点中删除该关键字 $k$ 。这个过程有点类似BST的删除操作。

# 优点

在磁盘等介质上进行读写时，如果树的深度过大则会产生大量的IO操作，因此需要减少树的高度。

同时，B树能够更的利用磁盘成块（扇区）读写的性质

# Java实现

实现了插入与删除功能

默认实现2-3树

关键字不可重复，代码内有注释以及assert作为提示。

package DataStructure.Tree;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;

public class BTree<K extends Comparable<K>> implements Tree<K> {

    private final int maxChildSize;
    private final int minChildSize;
    private final int maxKeySize;
    private final int minKeySize;

    private Node<K> root;

    public BTree() {
        this(3);
    }

    public BTree(int order) {
        maxChildSize = order;
        minChildSize = (order + 1) / 2;
        maxKeySize = maxChildSize - 1;
        minKeySize = minChildSize - 1;
        root = new Node<>(null);
    }

    @Override
    public void insert(K key) {
        // 找到第一个可以插入的叶子节点
        Node<K> current = root;
        while (true) {
            if (current.isLeaf()) {
                current.addKey(key);
                if (current.keySize > maxKeySize) {
                    splitNode(current);
                }
                break;
            }

            // 非叶子节点，找到第一个大于 key 的内部节点
            assert (current.keySize + 1 == current.childSize);
            int iter;
            for (iter = 0; iter < current.keySize; iter++) {
                if (current.keys[iter].compareTo(key) >= 0) break;
            }
            current = current.children[iter];
        }
    }

    @Override
    public void remove(K key) {
        Node<K> node = getNode(key);
        if (node != null) {
            if (node.isLeaf()) {
                node.removeKey(key);
                combine(node);
            } else {
                // 找到它的前驱
                int idxOfKey = node.indexOfKey(key);
                Node<K> greatestNode = node.children[idxOfKey];
                while (!greatestNode.isLeaf()) {
                    greatestNode = greatestNode.children[greatestNode.childSize - 1];
                }
                K greatestKey = greatestNode.keys[greatestNode.keySize - 1];

                node.keys[idxOfKey] = greatestKey;
                greatestNode.removeKey(greatestKey);
                combine(greatestNode);
            }
        }
    }

    @Override
    public List<K> travel() {
        List<K> result = new ArrayList<>();
        travel(result, root);
        return result;
    }

    /**
     * 修复删除关键字导致的节点关键字过少
     */
    private void combine(Node<K> node) {
        if (node.keySize >= minKeySize) return;
        if (node == root) return;

        Node<K> parent = node.parent;
        int nodeIdx = parent.indexOfChild(node);
        boolean usingPrecursor = nodeIdx != 0; // 兄弟节点是否是前驱（小于当前节点）
        int neighborIdx = nodeIdx + (usingPrecursor ? -1 : 1);

        // 在node与neighbor之间的key
        K parentKey = usingPrecursor ? parent.keys[nodeIdx - 1] : parent.keys[nodeIdx];
        Node<K> neighbor = parent.children[neighborIdx];
        parent.removeKey(parentKey);
        node.addKey(parentKey);

        if (neighbor.keySize > minKeySize) { // 从兄弟节点借
            K neighborKey = neighbor.keys[usingPrecursor ? neighbor.keySize - 1 : 0];
            neighbor.removeKey(neighborKey);
            parent.addKey(neighborKey);
            if (neighbor.childSize > 0) {
                Node<K> neighborChild = neighbor.children[usingPrecursor ? neighbor.childSize - 1 : 0];
                neighbor.removeChild(neighborChild);
                node.addChild(neighborChild);
            }
        } else { // 无法从兄弟节点借，合并
            parent.removeChild(neighbor);
            node.addKeys(neighbor.keys, 0, neighbor.keySize);
            node.addChildren(neighbor.children, 0, neighbor.childSize);
            // 除根节点外，每个节点至少有minKeySize个key
            if (parent.parent != null && parent.keySize < minKeySize) {
                combine(parent);
            } else if (parent.keySize == 0) {
                node.parent = null;
                root = node;
            }
        }
    }


    private void splitNode(Node<K> node) {
        assert (node.keySize >= 3);

        Node<K> parent = node == root ? new Node<K>(null) : node.parent;
        Node<K> left = new Node<K>(parent);
        Node<K> right = new Node<K>(parent);
        if (node == root) {
            root = parent;
        } else {
            parent.removeChild(node);
        }

        int mid = (node.keySize - 1) / 2;
        parent.addKey(node.keys[mid]);

        left.addKeys(node.keys, 0, mid);
        right.addKeys(node.keys, mid + 1, node.keySize);
        if (node.childSize > 0) {
            left.addChildren(node.children, 0, mid + 1);
            right.addChildren(node.children, mid + 1, node.childSize);
        }
        parent.addChild(left);
        parent.addChild(right);

        if (parent.keySize > maxKeySize) {
            splitNode(parent);
        }
    }

    private Node<K> getNode(K key) {
        Node<K> current = root;
        while (current != null) {
            int iter;
            for (iter = 0; iter < current.keySize; iter++) {
                int diff = current.keys[iter].compareTo(key);
                if (diff == 0) return current;
                if (diff > 0) break;
            }
            current = current.children[iter];
        }
        return null;
    }

    private void travel(List<K> result, Node<K> node) {
        if (node == null) return;
        for (int i = 0; i < node.keySize; i++) {
            travel(result, node.children[i]);
            result.add(node.keys[i]);
        }
        if (node.childSize > 0)
            travel(result, node.children[node.childSize - 1]);
    }

    private class Node<K extends Comparable<K>> {

        private K[] keys = (K[]) new Comparable[maxKeySize + 1];
        private Node<K>[] children = new Node[maxChildSize + 1];
        private int keySize = 0;
        private int childSize = 0;
        private Node<K> parent;
        private Comparator<Node<K>> comparator = new Comparator<Node<K>>() {
            @Override
            public int compare(Node<K> o1, Node<K> o2) {
                return o1.keys[0].compareTo(o2.keys[0]);
            }
        };

        private Node(Node<K> parent) {
            this.parent = parent;
        }

        private void addKey(K key) {
            keys[keySize++] = key;
            Arrays.sort(keys, 0, keySize);
        }

        private void addKeys(K[] arr, int from, int to) {
            for (int i = from; i < to; i++) {
                keys[keySize++] = arr[i];
            }
            Arrays.sort(keys, 0, keySize);
        }

        private void removeKey(K key) {
            boolean found = false;
            for (int i = 0; i < keySize; i++) {
                if (found) {
                    keys[i - 1] = keys[i];
                } else if (keys[i].compareTo(key) == 0) {
                    found = true;
                }
            }
            keySize--;
        }

        private void addChild(Node<K> child) {
            children[childSize++] = child;
            child.parent = this;
            Arrays.sort(children, 0, childSize, comparator);
        }

        private void addChildren(Node<K>[] arr, int from, int to) {
            for (int i = from; i < to; i++) {
                children[childSize++] = arr[i];
                arr[i].parent = this;
            }
            Arrays.sort(children, 0, childSize, comparator);
        }

        private void removeChild(Node<K> child) {
            boolean found = false;
            for (int i = 0; i < childSize; i++) {
                if (found) {
                    children[i - 1] = children[i];
                } else if (child == children[i]) {
                    found = true;
                }
            }
            childSize--;
        }

        private int indexOfChild(Node<K> child) {
            for (int i = 0; i < childSize; i++) {
                if (children[i] == child) return i;
            }
            throw new RuntimeException("未找到该子节点");
        }

        private int indexOfKey(K key) {
            for (int i = 0; i < keySize; i++) {
                if (keys[i].compareTo(key) == 0) return i;
            }
            throw new RuntimeException("未找到该关键字");
        }

        private boolean isLeaf() {
            return childSize == 0;
        }

        public String toString() {
            StringBuilder builder = new StringBuilder("keys: ");
            for (int i = 0; i < keySize; i++) {
                builder.append(keys[i]).append(" ");
            }
            return builder.toString();
        }

    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272

测试代码与AVL树的类似，略

# 参考资料

https://my.oschina.net/u/4116286/blog/3107389 （删除部分有误）
https://blog.csdn.net/qq_41078889/article/details/108756708
https://github.com/phishman3579/java-algorithms-implementation
https://en.wikipedia.org/wiki/B-tree

# B+树

B+树与B树类似，其不同点如下：

叶子节点保存关键字的全部信息，且叶子节点之间依据关键字大小相互链接（链表）
非叶子结点可以看做索引，存放的是对应子树中最小/最大关键字（一说是直接子节点的最小/最大关键字）

关于关键字个数的限制，在查阅资料后，发现有两种说法：

说法一：
- 内部节点的关键字个数等于子节点个数
说法二：
- 内部节点的关键字个数等于子节点个数-1（同B树）

另外，中文Wiki与英文Wiki中关于每个节点中关键字的最低数量有冲突，而英文wiki的参考资料又与wiki冲突，建议自行取舍。

# 优点

由于内部节点不需要保存完整信息，因此单一节点可以保存更多信息，IO次数更少。
叶节点形成链表，在范围查询时不需要进行中序遍历
查询数据必定要查找到叶子节点，性能稳定（这算优点？？？）

# 实现

与B树唯一的差别在于：

添加关键字时，若关键字个数过多需要分裂，要注意仅叶子节点需要保存值
删除关键字时，对于叶子节点，由于有兄弟节点的"指针"，因此可以不经父节点获取到兄弟节点
添加关键字时要沿途更新索引，删除关键字后要向根节点方向更新索引

# 参考资料

https://www.geeksforgeeks.org/introduction-of-b-tree/
https://en.wikipedia.org/wiki/B%2B_tree
https://zh.wikipedia.org/wiki/B%2B%E6%A0%91
https://segmentfault.com/a/1190000020416577

# 红黑树

红黑树是一棵自平衡二叉树，满足以下性质

任何节点要么是红色，要么是黑色
根节点是黑色（不重要）
所有叶子节点（NIL，不含任何数据）是黑色的
如果一个节点是红色的，则其子节点是黑色的
任意一个点到其子孙叶子节点的所有路径中，黑节点个数相同

由性质4/5可以看出：从根节点到所有叶子节点的路径中，最长的长度小于等于最短的两倍

一颗含有 $n$ 个节点的红黑树高度至多为 $2log(n+1)$

# 插入操作

插入时，先按普通二叉树的方式插入，并把插入的节点染成红色，此时显然不会违背性质1/2/3/5，因此只需检查性质4

当父节点是黑色节点

满足性质4，插入完成
当父节点是红色节点

由于根节点必定是黑色节点（性质二），而父节点是红色节点，因此必定有祖父节点（黑色），进而必定有叔叔节点（内部节点或NIL节点）
- 叔叔节点是红色
  
  将父节点、叔叔节点染为黑色，将祖父节点染为红色，并继续检查祖父节点是否满足性质4
- 叔叔节点是黑色
  - LR/RL型：在当前节点上进行一次旋转，使之变成LL/RR型
  - LL/RR型：
    
    对父节点进行一次旋转，并把父节点染成黑色，同时为了避免性质5被破坏，将原祖父节点染为红色（由于原叔叔节点是黑色，原兄弟节点是黑色，因而不会破坏性质4）

解决问题的关键在于不断将多余的红色节点向根节点方向移动

# 删除操作（较难理解，附图）

（删除总比插入难）

二叉树删除节点时，若被删除节点有2个非空子节点，总可以通过与前驱/后继交换值的方法，转换为删除至多只有一个非空孩子的节点，因此接下来只讨论删除至多只有一个非空孩子的节点

若该节点是红色的，删除它并不会破坏红黑树的性质，因而无需额外操作
若该节点是黑色的，且它的子节点是红色的，此时只需将子节点染为黑色即可保持性质5
若该节点是黑色的，且他的子节点是黑色时的情况：

此时该节点的子节点必定都是NIL（否则，一子节点为非叶子结点，此时违反性质5）

将该节点删去（用NIL代替），为了维持性质5，我们暂且认为新的NIL等价于2个黑色节点（图中用正方形表示）

如上图所示，图中使用蓝色代表黑色节点，白色代表黑色或红色节点（不得不吐槽一句，Visio真的不好用）

下面开始分类讨论
1. brother为黑色，且brother有一个红色子节点，如下图所示
  
  如果红色节点与其父节点、祖父节点形成LR/RL型结构，则需要进行一次旋转（并重新染色）转化为LL/RR型，如上图(1)所示
  
  对于LL/RR型，则旋转兄弟节点，原父节点与兄弟节点交换颜色，并将子节点染为黑色（如上图(2)所示），相当于从兄弟节点借了一个黑色节点
2. brother为黑色，且无红色子节点
  
  如图所示，若parent为红色，则重新染色即可
  
  否则，将特殊节点上移并重新染色，若parent不为根节点，则需要继续对parent进行修复
3. 若brother为红色
  
  如图所示，旋转brother并重新染色，此时node的兄弟节点必定是黑色，转化为情况1/2

# Java实现

测试未通过

package DataStructure.Tree;

import com.sun.istack.internal.Nullable;

import java.util.ArrayList;
import java.util.List;

public class RedBlackTree<T extends Comparable<T>> implements Tree<T> {

    Node<T> root;

    @Override
    public void insert(T key) {
        if (root == null) {
            root = new Node<T>(null, key, Node.BLACK);
        } else {
            // 按照普通二叉树的方法插入
            Node<T> cur = root;
            while (true) {
                int direction = cur.key.compareTo(key);
                if (direction == 0) return;
                direction = direction < 0 ? 1 : 0;
                if (cur.children[direction] == null) {
                    Node<T> newNode = new Node<T>(cur, key, Node.RED);
                    cur.children[direction] = newNode;
                    balanceAfterInsertion(newNode);
                    break;
                }
                cur = cur.children[direction];
            }
        }
    }

    @Override
    public void remove(T key) {
        Node<T> toRemoved = getNode(key);
        if (toRemoved == null) return;
        // 当需要删除根节点，且根节点只有一个非空子节点
        if (toRemoved == root && (toRemoved.children[0] == null || toRemoved.children[1] == null)){
            root = root.children[0] == null ? root.children[1] : root.children[0];
            if(root != null) root.color = Node.BLACK;
            return;
        }

        if (toRemoved.children[0] != null && toRemoved.children[1] != null) {
            Node<T> successor = getSuccessor(toRemoved);
            toRemoved.key = successor.key;;
            toRemoved = successor;
        }

        if(toRemoved.children[0] != null && toRemoved.children[1] != null)
            throw new IllegalStateException("impossible");

        Node<T> childOfRemoved = null;
        if (toRemoved.children[0] != null) {
            childOfRemoved = toRemoved.children[0];
        } else {
            childOfRemoved = toRemoved.children[1];
        }

        setChild(toRemoved.parent, childOfRemoved, getDirection(toRemoved));
        if (toRemoved.color == Node.BLACK) {
            if (childOfRemoved != null && childOfRemoved.color == Node.RED) {
                childOfRemoved.color = Node.BLACK;
            } else {
                if(childOfRemoved != null) throw new IllegalStateException("childOfRemoved应当是null");
                balanceAfterDeletion(childOfRemoved, toRemoved.parent);
            }
        }
    }

    @Override
    public List<T> travel() {
        List<T> result = new ArrayList<>();
        travel(result, root);
        return result;
    }

    private void balanceAfterInsertion(Node<T> node) {
        if (node.parent == null) {
            node.color = Node.BLACK;
            return;
        }

        if (node.parent.color == Node.RED && node.color == Node.RED) {
            if (node.parent.parent == null) throw new IllegalStateException("应当存在祖父节点");
            Node<T> uncle = getUncle(node);
            Node<T> parent = node.parent;
            char uncleColor = uncle == null ? Node.BLACK : uncle.color;
            if (uncleColor == Node.RED) {
                uncle.color = Node.BLACK;
                parent.color = Node.BLACK;
                parent.parent.color = Node.RED;
                balanceAfterInsertion(parent.parent);
            } else {
                int parentDirection = getDirection(parent);
                int selfDirection = getDirection(node);

                if (selfDirection != parentDirection) { // LR型或RL型
                    rotate(node);
                    // 旋转后，parent已经变成了node的子节点
                    Node<T> tmp = parent;
                    parent = node;
                    node = tmp;
                }
                // LL/RR
                Node<T> grandParent = parent.parent;
                rotate(parent);
                // 旋转后，grandParent变为parent的子节点
                parent.color = Node.BLACK;
                grandParent.color = Node.RED;
            }
        }
    }

    /**
     * 删除节点后重新平衡子树
     * @param node 当前节点
     * @param parent 由于当前节点可能为null，因此需要提供父节点
     */
    private void balanceAfterDeletion(@Nullable Node<T> node, Node<T> parent) {
        if(node == root) return;

        int selfDirection = parent.children[0] == node ? 0 : 1;
        int brotherDirection = selfDirection ^ 1;
        Node<T> brother = parent.children[brotherDirection];
        if (brother == null) throw new IllegalStateException("兄弟节点不可能为空");

        if(brother.color == Node.BLACK){
            int redChildOfBrother = -1;
            if (brother.children[selfDirection] != null &&
                    brother.children[selfDirection].color == Node.RED) {
                redChildOfBrother = selfDirection;
            }
            if (brother.children[brotherDirection] != null &&
                    brother.children[brotherDirection].color == Node.RED) {
                redChildOfBrother = brotherDirection;
            }

            if(redChildOfBrother == selfDirection){ // LR/RL, 转为LL/RR型
                Node<T> redChild = brother.children[redChildOfBrother];
                rotate(redChild);
                brother.color = Node.RED;
                redChild.color = Node.BLACK;
                brother = redChild;
                redChildOfBrother = brotherDirection;
            }

            if(redChildOfBrother == brotherDirection){ // LL/RR
                Node<T> redChild = brother.children[redChildOfBrother];
                rotate(brother);
                redChild.color = Node.BLACK;
                brother.color = parent.color;
                parent.color = Node.BLACK;
            }else{ // 兄弟节点无红色子节点
                if(parent.color == Node.RED){
                    parent.color = Node.BLACK;
                    brother.color = Node.RED;
                }else{
                    brother.color = Node.RED;
                    balanceAfterDeletion(parent, parent.parent);
                }
            }

        }else{ // 兄弟节点为红色
            rotate(brother);
            brother.color = Node.BLACK;
            parent.color = Node.RED;
            balanceAfterDeletion(node, parent);
        }

    }

    /**
     * 对当前节点进行旋转（左旋或右旋），使其与父节点交换位置
     */
    private void rotate(Node<T> node) {
        if (node.parent == null) throw new IllegalStateException("不能旋转根节点");

        Node<T> parent = node.parent;
        Node<T> grandParent = parent.parent;
        int selfDirection = getDirection(node);

        setChild(grandParent, node, grandParent == null ? -1 : getDirection(parent));
        setChild(parent, node.children[selfDirection ^ 1], selfDirection);
        setChild(node, parent, selfDirection ^ 1);

        if (grandParent == null) {
            root = node;
        }
    }

    private void setChild(@Nullable Node<T> parent, @Nullable Node<T> child, int direction) {
        if (parent != null) parent.children[direction] = child;
        if (child != null) child.parent = parent;
    }

    /**
     * 获取当前节点的叔叔节点
     *
     * @return 如果叔叔节点不存在，则返回null
     */
    private Node<T> getUncle(Node<T> node) {
        Node<T> grandParent = node.parent.parent;
        return grandParent.children[getDirection(node) ^ 1];
    }

    /**
     * 获取当前节点对于父节点的方向
     *
     * @return 如果当前节点为父节点的左子节点，则返回0，否则返回1
     */
    private int getDirection(Node<T> node) {
        assert (node != root);
        return node.parent.children[0] == node ? 0 : 1;
    }

    private Node<T> getNode(T key) {
        Node<T> node = root;
        while (node != null) {
            int diff = node.key.compareTo(key);
            if (diff == 0) return node;
            node = node.children[diff < 0 ? 1 : 0];
        }
        return null;
    }

    /**
     * 寻找当前子树下的后继，若不存在则返回null
     */
    private Node<T> getSuccessor(Node<T> node) {
        node = node.children[1];
        while (node.children[0] != null) node = node.children[0];
        return node;
    }

    /**
     * 中序遍历
     */
    private void travel(List<T> result, Node<T> node) {
        if (node == null) return;
        travel(result, node.children[0]);
        result.add(node.key);
        travel(result, node.children[1]);
    }

    private static final class Node<T extends Comparable<T>> {

        static final char BLACK = 0;
        static final char RED = 1;

        Node<T> parent;
        Node<T> children[] = new Node[2];
        T key;
        char color = BLACK;

        Node(Node<T> parent, T key, char color) {
            this.parent = parent;
            this.key = key;
            this.color = color;
        }

    }
}

# 参考资料

https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91
https://www.cnblogs.com/skywang12345/p/3245399.html
https://www.tianxiaobo.com/2018/01/11/%E7%BA%A2%E9%BB%91%E6%A0%91%E8%AF%A6%E7%BB%86%E5%88%86%E6%9E%90/
https://segmentfault.com/a/1190000012115424（推荐阅读）

# 其他树（线段树/LinkCutTree/Splay等）

见算法学习-数据结构一栏

上次更新: 2021/03/27, 23:40:59