Chgtaxihe's blog

凸包学习笔记

# 前置小知识

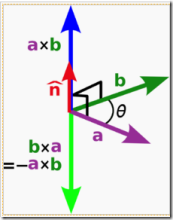
叉积：

a⃗×b⃗=∣a⃗∣∣b⃗∣sinθ=x1y2−x2y1(0<θ≤2π)\vec a \times \vec b=\mid\vec a\mid\mid\vec b\mid sin\theta=x_1y_2-x_2y_1\ (0\lt\theta\le2\pi)

其中θ\theta为a⃗\vec a沿逆时针方向与b⃗\vec b形成的夹角

右手定则：

c=a×bc=a\times b，当右手的四指aa以不超过180度转交转向bb，大拇指指向的便是cc的方向

Ypne91.png

# Graham算法模板

所谓学习笔记，不过是模板而已[1]

洛谷P2742: 求凸包的周长

#include <bits/stdc++.h>
#define ll long long
#define Android ios::sync_with_stdio(false), cin.tie(NULL)

using namespace std;

const int max_node = 1e5 + 100;
struct point{
    double x, y;
    bool operator <(const point & p)const{return (y==p.y)?(x<p.x):(y<p.y);}
};
struct vec{
    double x, y;
    vec(){}
    vec(double a, double b):x(a),y(b){}
    vec(point & from, point & to){x = to.x-from.x, y = to.y-from.y;}
    vec operator +(const vec & p)const{return vec(x+p.x, y+p.y);}
    vec operator -(const vec & p)const{return vec(x-p.x, y-p.y);}
    double operator *(const vec & p)const{return x*p.y - y*p.x;}
    double length(){return sqrt(x*x+y*y);}
};

vector<point> convex_hull(vector<point> pts){
    int steck[max_node], head=0; // 手工栈
    for(int i=1; i<pts.size(); i++){
        if(pts[i] < pts[0]) swap(pts[i], pts[0]);
    }
    point base = pts[0];
    sort(pts.begin()+1, pts.end(), [&](point x1, point x2){
        vec v1(base, x1), v2(base, x2);
        double k = v1 * v2;
        return k==0?v1.length()<v2.length():k>0; // 按辐角排序，相同则短者优先
    });
    steck[head++] = 0;
    for(int i=1; i<pts.size(); i++){
        while(head > 1 && vec(pts[steck[head-2]], pts[steck[head-1]])*vec(pts[steck[head-1]], pts[i])<=0) head--;
        steck[head++] = i;
    }
    vector<point> ret(head);
    for(int i=0; i<head; i++) ret[i] = pts[steck[i]];
    return ret;
}

void solve(){
    int n;
    cin >> n;
    vector<point> pts(n);
    for(int i=0; i<n; i++) cin >> pts[i].x >> pts[i].y;
    pts = convex_hull(pts);
    double ans = 0;
    for(int i=1; i<pts.size(); i++){
        vec v(pts[i], pts[i-1]);
        ans += v.length();
    }
    ans += vec(pts[pts.size()-1], pts[0]).length();
    cout << fixed << setprecision(2) << ans << endl;
}

signed main(){
    Android;
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

# 旋转卡壳（单调性优化）

用于求凸包直径（凸包上最远点对距离/图上最远点对的距离）

首先建出凸包，逆时针遍历凸包上的边eie_i。

对于边eie_i，若使得三角形面积最大的点为pjp_j，且对于边ei+1e_{i+1}，使得三角形面积最大的点pkp_k，定有k≥jk\ge j

详细解析见[2]

例题：洛谷P1452

#include <bits/stdc++.h>
#define ll long long
#define Android ios::sync_with_stdio(false), cin.tie(NULL)
#define debug(s, r) std::cerr << #s << ": " << (s) << (r==0?' ':'\n')
#define pii pair<int, int>  
#define sqr(x) ((x)*(x))

using namespace std;

const int max_node = 1e5 + 100;
// 求凸包的模板，此处省略

void solve(){
    int n;
    cin >> n;
    vector<point> pts(n);
    for(int i=0; i<n; i++) cin >> pts[i].x >> pts[i].y;
    pts = convex_hull(pts);
    if(pts.size() == 2){
        cout << (ll)(sqr(pts[0].x-pts[1].x) + sqr(pts[0].y-pts[1].y)) << endl;
        return;
    }

    // 旋转卡壳开始
    pts.push_back(pts[0]); // 第一个点加到最后
    int j = 2, sz = pts.size();
    ll ans = 0;
    for(int i=0; i<sz-1; i++){
        vec edge = vec(pts[i], pts[i+1]);
        double tmp = edge * vec(pts[i], pts[j]), ttmp = edge * vec(pts[i], pts[(j+1)%sz]);
        while(tmp <= ttmp){
            if(tmp == ttmp){ // 高相同时(面积相同)，距离不一定相同
                ans = max(ans, (ll)(sqr(pts[i].x-pts[j].x) + sqr(pts[i].y-pts[j].y)));
                ans = max(ans, (ll)(sqr(pts[i+1].x-pts[j].x) + sqr(pts[i+1].y-pts[j].y)));
            }
            j=(j+1) % sz;
            tmp = edge * vec(pts[i], pts[j]), ttmp = edge * vec(pts[i], pts[(j+1)%sz]);
        }
        ans = max(ans, (ll)(sqr(pts[i].x-pts[j].x) + sqr(pts[i].y-pts[j].y)));
        ans = max(ans, (ll)(sqr(pts[i+1].x-pts[j].x) + sqr(pts[i+1].y-pts[j].y)));
    }
    cout << ans << endl;
}

signed main(){
    Android;
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 例题 Gym102460L

AC代码

该题必须用LL，用double容易Wa5

#include <bits/stdc++.h>
#define ll long long
#define Android ios::sync_with_stdio(false), cin.tie(NULL)
#define sqr(x) ((x)*(x))

using namespace std;

const int max_node = 4096 + 100;
struct point{
    ll x, y;
    bool operator ==(const point & p)const{return x==p.x && y==p.y;}
    bool operator !=(const point & p)const{return x!=p.x || y!=p.y;}
    bool operator <(const point & p)const{return (y==p.y)?(x<p.x):(y<p.y);}
};
struct vec{
    ll x, y;
    vec(){}
    vec(ll a, ll b):x(a),y(b){}
    vec(point & from, point & to){x = to.x-from.x, y = to.y-from.y;}
    vec operator +(const vec & p)const{return vec(x+p.x, y+p.y);}
    vec operator -(const vec & p)const{return vec(x-p.x, y-p.y);}
    ll operator *(const vec & p)const{return x*p.y - y*p.x;}
    double length(){return sqrt(x*x+y*y);}
};

vector<point> convex_hull(vector<point> pts){
    int steck[max_node], head=0;
    for(int i=1; i<pts.size(); i++){
        if(pts[i] < pts[0]) swap(pts[i], pts[0]);
    }
    point base = pts[0];
    sort(pts.begin()+1, pts.end(), [&](point x1, point x2){
        vec v1(base, x1), v2(base, x2);
        double k = v1 * v2;
        return k==0?v1.length()<v2.length():k>0;
    });
    steck[head++] = 0;
    for(int i=1; i<pts.size(); i++){
        while(head > 1 && vec(pts[steck[head-2]], pts[steck[head-1]])*vec(pts[steck[head-1]], pts[i])<=0) head--;
        steck[head++] = i;
    }
    vector<point> ret(head);
    for(int i=0; i<head; i++) ret[i] = pts[steck[i]];
    return ret;
}

int sz;
int nxt(int k){return (k+1)%sz;}
ll areaa(point & a, point & b, point & c){
    return vec(a, c) * vec(a, b);
}
void solve(){
    int n;
    cin >> n;
    vector<point> pts(n);
    for(int i=0; i<n; i++) cin >> pts[i].x >> pts[i].y;
    vector<point> convex_pts = convex_hull(pts);
    ll ans = 0;
    if(convex_pts.size() <= 2){
        ans = 0;
    }else if(convex_pts.size() == 3){
        ll area = abs(areaa(convex_pts[0], convex_pts[1], convex_pts[2]));
        ll mn = area;
        vector<int> idx;
        for(int i=0; i<3; i++){
            for(int j=0; j<pts.size(); j++){
                if(pts[j] == convex_pts[i]) {
                    idx.push_back(j);
                    break;
                }
            }
        }
        for(int i=0; i<pts.size(); i++){
            if(i == idx[0] || i == idx[1] || i == idx[2]) continue;
            for(int j=0; j<3; j++){
                mn = min(mn, abs(areaa(convex_pts[j], convex_pts[(j+1)%3], pts[i])));
            }
        }
        ans = area - mn;
    }else{
        sz = convex_pts.size();
        for(int i=0; i<sz; i++){
            int p1 = nxt(i), p2 = nxt(nxt(nxt(i)));
            for(int j=nxt(nxt(i)); nxt(j)!=i; j=nxt(j)){
                point & pi = convex_pts[i], &pj = convex_pts[j];
                while(nxt(p1) != j && areaa(pi, pj, convex_pts[p1]) < areaa(pi, pj, convex_pts[nxt(p1)])) p1 = nxt(p1);
                while(nxt(p2) != i && areaa(pi, convex_pts[p2], pj) < areaa(pi, convex_pts[nxt(p2)], pj)) p2 = nxt(p2);
                ans = max(ans, areaa(pi, pj, convex_pts[p1]) + areaa(pi, convex_pts[p2], pj));
            }
        }
    }
    if(ans & 1){
        cout << ans / 2 << ".5\n";
    }else{
        cout << ans/2 << endl;
    }
}

signed main(){
    Android;
    int t; cin >> t;
    while(t--)
    solve();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

# 参考

[1]https://www.luogu.com.cn/blog/ShineEternal/convex-hull

[2]https://blog.csdn.net/engineoid/article/details/104128809

上次更新: 2021/02/24, 03:37:30
几何模板
多边形面积

← 多边形面积→

最近更新
01
深入理解Java虚拟机
 03-04
02
DNS工作原理
 02-27
03
改用VuePress啦
 02-23
更多文章>
Theme by Vdoing | Copyright © 2019-2021