Codeforces 刷题计划~

说明

有些题目比较简单，就没写题解/AC代码啦

UPD: 我好菜啊

Div. 1

Codeforces Round #609

题解 (opens new window)

题号	完成	备注	过题人数
D. Invertation in Tournament		我不配 ╥﹏╥	93
E. Happy Cactus			58

Codeforces Round #631

题号	完成	备注	过题人数
A. Dreamoon Likes Coloring	AC(WA14/21)		1666
B. Dreamoon Likes Sequences	AC(TLE3)	记忆化搜索	1735
C. Drazil Likes Heap	AC	贪心+模拟（细节多）	833
D. Dreamoon Likes Strings	题解		112
E. Dreamoon Loves AA			34

B题题解

这题不需要搜索

设$h(x)$为$x$的二进制的最高位位置，如$h(1)=0,h(2)=h(3)=1$，那么显然有$h(a_i)<h(a_j)\ (i<j)$

那么对于每一位$v(0\le v\le h(d))$，可以有两类情况：

1. 选：则有$min(2^{v+1}-1,d)-2^v+1$中情况
2. 不选，有1中情况

则该位有$c(v)=min(2^{v+1}-1,d)-2^v+2$种情况

则答案$ans=-1+\prod_{i=0}^{h(d)}c(i)$，之所以要减一是因为要剔除序列长度为0的情况

原理大致同我的dfs搜索一样，但快得多~

---

C题题解

这题正解不是模拟。

注意：

1. 假设这棵树剩下的元素组成的集合$s$已经确定，那么这棵树的形状就是唯一确定的。

2. 假如一个数$x$不在最终的序列$s$中，那么一定进行过$f(pos_x)$。因此，操作的序列可以由一下方式得出

   bool in_final_set[maxn];
   vector<int> ans;
   for(int i=n; i>=1; i--){
       if(!in_final_set[i]) ans.push_back(i);
   }
   

   $ans$即为操作序列

3. 这里有一份更“优雅”的模拟，代码更短，耗时更短(358ms)！

AC代码 (opens new window)

---

D题题解

根据题解，最小的操作数为$max(\lceil \frac{\sum c_i}{2} \rceil, max_{0\le i\le25}(c_i)) + 1$

把$s_i=s_{i+1}$的$i$称为隔板，可以发现每次操作，如果存在其他不同颜色的隔板，那么我们可以一次消除2个隔板，否则只能一个一个地消。消去所有隔板后，序列仍不为空，还需要一次操作来清空序列，这就是最小操作数式子的由来。

参考 (opens new window)（对大佬而言" 思维难度基本上没有 "，o(╥﹏╥)o）

Codeforces Round #633

题号	完成	备注	过题人数
A. Powered Addition	AC(WA3)		2000
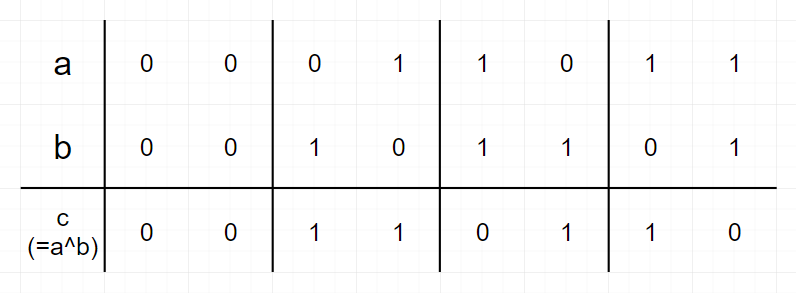
B. Edge Weight Assignment	题解AC	巧妙构造/边权转化为两点权异或	1683
C. Perfect Triples	题解AC	真的是神仙题	1184
D. Nested Rubber Bands			299
E. JYPnation			35

B题代码 (opens new window)

---

C题题解

考虑$[1, 4^n-1]$的数字已经全部使用，那么一定有$a_{2n}=1, a_{2n+1}=0, b_{2n}=0, b_{2n+1}=1$，其中$a_x,b_x$分别代表$a、b$二进制表示的第$x$位

如下图所示

因而对于$a$的$(i+1,i)(i\in \{0, 2, 4, 6, ...\})$位，有4种取法，每种取法都有唯一对应的$b_{i+1},b_{i},c_{i+1},c_i$，按照这种方法同时可保证把$[1, 4^n-1]$的所有数字用完

AC代码 (opens new window)

Codeforces Round #618

题号	完成	备注	过题人数
A. Anu Has a Function)	题解AC	$(a\mid b)-b=a\&(\sim b)$，注意用unsigned和&与>的优先级	1881
B. Aerodynamic	题解AC	又是一道神仙题	1403
C. Water Balance	题解AC	差点...	1327
D. Around the World			177
E. So Mean			51

B题题解

（基本上是翻译）

Convex Polygon指凸多边形（任意一条边无限延长为直线时，其他各边都在此直线同旁）

如果$\{(x_0,y_0), (0,0)\}\in P(x,y)$，那么$\{(-x_0,-y_0), (0,0)\}\in P(x-x_0,y-y_0)$，因此，$T$中心对称。如果$S\sim T$，必有$S$中心对称。

下面证明如果S中心对称，则S的每条边放大到原来的2倍后与T全等

首先平移$S$，使得$S$的对称中心与$(0,0)$重合。

1. 如果$(x_0,y_0)\in P$，那么$\{(0,0),(2x_0,2y_0)\}\in P(x_0,y_0)$
2. 如果$(x_0,y_0)\not\in P$，那么线段$\{(0,0),(x_0,y_0)\}$一定穿过$P$的某一条边$e_0$，下面我们称与$e_0$中心对称的边为$e_0'$。由于$S$是凸多边形，我们把$e_0,e_0'$沿两端无限延长成直线，进而$S$的所有点都夹在$e_0,e_0'$之间，将所有点$(x,y)$放大一倍后，点$(2x_0,2y_0)$定不在新边$e_1,e_1'$范围内。

对称性的判断见代码。

AC代码 (opens new window)

---

D题题解

一开始就往斜率的方向考虑， 但是没有发现$a$的什么性质...

看了题解之后，发现可以用前缀和$pre_i$来代替$a_i$，显然如果序列$S$是字典序最小的，那么它对应的前缀和序列也是字典序最小的，反之亦然。又因为$a_i\ge 1$，所以$pre_i$单调递增。

将$x=i,y=pre_i$画出来，考虑进行一次操作$[l,r]$，就相当于使得$p_i=p_{l-1}+\frac{p_r-p_l}{r-l+1}(i-l+1)$，那么要使得$p_i$字典序最小，每次变换都选择一个斜率最小的即可，有点类似斜率dp。

AC代码 (opens new window)

Codeforces Round #616

题号	完成	备注	过题人数
A. Mind Control	AC	想到了暴力，但是没敢做，姑且算自己AC吧	1497
B. Irreducible Anagrams	题解AC	题解的证明很有意思	1251
C. Prefix Enlightenment	看题解+代码AC	2-SAT?不不不	719
D. Coffee Varieties (hard version)			248
E. Cartesian Tree			64
F. Making Shapes			40

A题AC代码 $O(n^2)$ (opens new window)

A题AC代码 $O(n)$ (opens new window)

---

C题每个开关只有两个状态，同时一个点$x$最多只会被两个开关$(a,b)$控制，根据$x$的初始状态便可确定$(a,b)$的相对状态（如果$x=off$，则$a,b$有且只有一个被操作，反之$x=on$，$a,b$要么同时操作，要么同时不被操作），对每个开关建两个点，分别代表操作/不操作，并用dsu维护联通集，同时维护一个联通集内所需操作数。显然$a_{on},a_{off}$一定是不联通的，那么求答案的时候取一下$min(size[block(a_{on})], size[block(a_{off})])$即可

C题AC代码 (opens new window)

Codeforces Round #614

题号	完成	备注	过题人数
A. NEKO's Maze Game	AC	水	2138
B. Aroma's Search	题解AC(WA49)		1456
C. Xenon's Attack on the Gangs			877
D. Chaotic V.			400
E. Rin and The Unknown Flower			90
F. Nora's Toy Boxes			44

B题AC代码 (opens new window)

Div. 2

Codeforces Round #588

题解 (opens new window) VirtualJudge (opens new window)

我的AC代码(C/D/E/F) (opens new window)

题号	完成	一句话题解
A. Dawid and Bags of Candies	√
B. Ania and Minimizing	√
C. Anadi and Domino	√	如果n = 7，那么一定有两个点公用一个数字
D. Marcin and Training Camp	√	如果A和B不是子集关系，那么A比B强且B比A强，$O(n^2)$
E. Kamil and Making a Stream	√	AC容易，证明复杂度不易($v$到$v$的祖先路径上的不同的$gcd$不会超过$log(10^12)$个)
F. Konrad and Company Evaluation	√	$ans = \sum OutDegree_i * InDegree_i$ 难点在于证明复杂度$O(n + m + q \sqrt{2m})$

Educational Codeforces Round 73

(Virtual Participate)

题号	完成	一句话题解	过题人数
A. 2048 Game	√		5662
B. Knights	√	随便猜个结论，居然过了？？？	4135
C. Perfect Team	√		4776
D. Make The Fence Great Again	√	每个板子增加的长度不会超过2，故$dp_{pos, add} = add \cdot b_{pos} + \min\limits_{x=0 \dots 2, a_{pos-1}+x \neq a_{pos}+add} dp_{pos-1, x}$	1426
E. Game With String	√	不容易啊，题解 (opens new window)	122
F. Choose a Square	╳		85
G. Graph And Numbers	╳		12

Codeforces Round #589

题解 (opens new window) VirtualJudge (opens new window)

我的AC代码(C/D/E) (opens new window)

题号	完成	一句话题解	过题人数
A. Distinct Digits	√		10912
B. Filling the Grid	√	暴力模拟	6921
C. Primes and Multiplication	√	数学太恐怖，去看题解吧	4559
D. Complete Tripartite	√	优雅的暴力	2842
E. Another Filling the Grid	√	[DP] 题解表述有误，看评论区	965
F. One Node is Gone			209

Educational Codeforces Round 74

题解 (opens new window)

我的AC代码(D) (opens new window)

题号	完成	一句话题解	过题人数
A. Prime Subtraction	√		6751
B. Kill `Em All	√		4535
C. Standard Free2play	√	讨论所有1序列的长度	2388
D. AB-string	√	字符串只由AB组成，最后计算的方法也有意思	1137
E. Keyboard Purchase			263
F. The Maximum Subtree			167
G. Adilbek and the Watering System			15

Codeforces Round #592

题解 (opens new window)

我的AC代码(B/C/E) (opens new window)

题号	完成	一句话题解	过题人数
A. Pens and Pencils (opens new window)	√		10601
B. Rooms and Staircases (opens new window)	√	[贪心]我好菜	8449
C. The Football Season (opens new window)	√	[数论]因为平局w场 = 赢d场所以如果有解，定有平局数 <= w的解，当然也可以用exgcd(Wa了10发)	3966
D. Paint the Tree (opens new window)	√	[图论]比C简单太多了	3634
E. Minimizing Difference (opens new window)	√	[思维]最小值/最大值中一个 一定是原序列中的值	2432
F. Chips (opens new window)			799
G. Running in Pairs (opens new window)			764

Codeforces Round #593

题解 (opens new window)

我的AC代码(C/D) (opens new window)

题号	完成	一句话题解	通过人数
A. Stones (opens new window)	√		9451
B. Alice and the List of Presents (opens new window)	√	智障了，没想出来	5826
C. Labs (opens new window)	√	[贪心]最优解为$\lfloor\frac{n^2}{2}\rfloor$	5886
D. Alice and the Doll (opens new window)	√	[贪心] + [模拟] 细节巨多	1103
E. Alice and the Unfair Game (opens new window)			331
F. Alice and the Cactus (opens new window)			29

Codeforces Round #594

题解 (opens new window)

我的AC代码(C) (opens new window)

题号	完成	一句话题解	通过人数
A. Integer Points (opens new window)	√		7454
B. Grow The Tree (opens new window)	√	[数学推导] $a^2 + b^2 < (a+1)^2 + (b-1)^2(a \ge b)$	7620
C. Ivan the Fool and the Probability Theory (opens new window)	√	[数学] + [找规律]十分值得做！！！	2760
D1. The World Is Just a Programming Task (Easy Version) (opens new window)			1262
D2. The World Is Just a Programming Task (Hard Version) (opens new window)			197
E. Queue in the Train (opens new window)			231
F. Catowice City (opens new window)			252

Educational Codeforces Round 75

题解 (opens new window)

我的AC代码(C/D) (opens new window)

题号	完成	一句话题解	通过人数
A. Broken Keyboard (opens new window)	√		5994
B. Binary Palindromes (opens new window)	√	[找规律]观察	3640
C. Minimize The Integer (opens new window)	√	[贪心]	2632
D. Salary Changing (opens new window)	√	想到思路敲不出来，那么不妨用暴力简化一下Coding复杂度	985
E1. Voting (Easy Version) (opens new window)			227
E2. Voting (Hard Version) (opens new window)			181
F. Red-White Fence (opens new window)			28

Codeforces Round #597

题解 (opens new window)

我的AC代码(D) (opens new window)

题号	完成	一句话题解	通过人数
A. Good ol' Numbers Coloring (opens new window)	√	[数学] 转化成数学式子，如a + b一定是白色的.结论: 如果$gcd(a, b) = 1$ 则 x是白色的 $(x>a*b)$,否则定存在 $x \bmod gcd(a,b) \neq 0$ 使得 $ax+by\neq x$	8460
B. Restricted RPS (opens new window)	√	题目很简单，但是比较考代码功底，基础差一点的写出来的代码就是乱七八糟(结果正确，只不过实现得很难看而已)	6982
C. Constanze's Machine (opens new window)	√	显而易见的DP题	6241
D. Shichikuji and Power Grid (opens new window)	√	想到了方法但是敲不出来，往往是因为思路混乱，又或是做法未经简化。两种做法: 1. 设计一个代价函数$C(u, v)$来跑最小生成树 2. 与其建一个森林(图论)，不如引入一个新的点将森林的根连接起来，然后最小生成树	2852
E. Hyakugoku and Ladders (opens new window)			680
F. Daniel and Spring Cleaning (opens new window)			886

Codeforces Round #599

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	一句话题解	通过人数
A. Maximum Square (opens new window)	√	排序	9682
B1. Character Swap (Easy Version) (opens new window)	√	分类讨论	8321
B2. Character Swap (Hard Version) (opens new window)	√	看代码/题解吧	3932
C. Tile Painting (opens new window)	√	[数论]见下	5258
D. 0-1 MST (opens new window)	√	正确估计复杂度 + 实现	1754
E. Sum Balance (opens new window)			198

C题题解

对于$n=p^k$(p为质数)，有$ans = p$ (A)

对于$n = pq$ ($gcd(p, q) = 1$)，有$ans=1$ (B)

下面对(B)进行证明

对于任意$i$和$j(i\neq j)$，存在$1 \le x \le n$使得$x \equiv i \pmod{p}$且$x \equiv j \pmod{q}$(中国剩余定理)

因此$i$和$j(i\neq j)$颜色与$x$相同

---

D题题解

暴力即可(set/bitset记录连通块)

Educational Codeforces Round 76

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	一句话题解	通过人数
A. Two Rival Students (opens new window)	√		7551
B. Magic Stick (opens new window)	√		6573
C. Dominated Subarray (opens new window)	√	贪心	5177
D. Yet Another Monster Killing Problem (opens new window)	√	[思维]需要注意到$1\leq s \leq n$(BTW, 用Python AC的代码基本都是压着时限卡过去的)	1728
E. The Contest (opens new window)			748
F. Make Them Similar (opens new window)			142
G. Divisor Set (opens new window)			34

Codeforces Round #600

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Single Push	√		8804
B. Silly Mistake	√		5743
C. Sweets Eating	√		5690
D. Harmonious Graph	√	题解的思路比我的更简单易懂(更优)	4046
E. Antenna Coverage	√	[Dp]	1464
F. Cheap Robot			520

Codeforces Round #601

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Changing Volume	√		9713
B. Fridge Lockers	√		6467
C. League of Leesins	√		3659
D. Feeding Chicken	√	python3的builtdins.input()比pypy3的快	1842
E1. Send Boxes to Alice (Easy Version)	√		1213
E2. Send Boxes to Alice (Hard Version)	√	对$a$求前缀和$S_i$，那么$box_i$向$box_{i+1}$移动一块，相当于$S_i -= 1$，对于$factor_k$,使得$all(S_i\%factor_k=0)$即可	604
F. Point Ordering			142

Educational Codeforces Round 77

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Heating	√		5450
B. Obtain Two Zeroes	√	对于$(a+b)\equiv0\pmod{3}$,定有$2a\equiv b\pmod3$(枚举一下$a$和$b$即可证明)故本题只需要满足$(a+b)\equiv 0\pmod3$和$min(a,b)*2\ge max(a,b)$即可	4380
C. Infinite Fence	√		2075
D. A Game with Traps	√	注意到：对与一个要排除的陷阱$(l_k, r_k, d_k)$，若$l_k <= r_k$，则我们需要经过区域$[l_k, r_k]$三次（人生苦短，我用C++）	796
E. Tournament			194
F. Colored Tree			20

C题题解

假定$r\le b$， $g=gcd(r, b)$，存在$rx - by = g$ ($y\ge0$)，即$rx = g + by$ ($y\ge0$)

则对于两个相邻的蓝色块$by$与$by + b$，我们要在其中插入$m+1$个红色块，

$by+g, by+g+r, by+g+2r,...,by+g+(m*r)$

且 $by+g+(m*r) < by+b$

也就是说$m+1 \ge k$，即$g + (k-1)*r < b$ 时REBEL，否则OBEY

Codeforces Round #603

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Sweet Problem	√	若$a\ge b\ge c$且$a \le b+c$，则按照最优策略，最后剩下的总糖果数为0或1	8681
B. PIN Codes	√		5919
C. Everyone is a Winner!	√	所有$k = \lfloor \sqrt{n} \rfloor$都属于是答案的一部分	6194
D. Secret Passwords	√		5144
E. Editor	√	第一反应是线段树，题解用两个stack维护左右两侧信息	1629
F. Economic Difficulties			448

F题题解

以cursor为界，分为左右两部分。同时计算左侧前缀和、右侧后缀和("("计1，")"计-1)。

若左侧合法，则定有$min(sum_{left}) \ge 0$，右侧合法则定有$max(sum_{right}) \le 0$

若整个串合法，除上述条件外，$sum_{left} + sum_{right}=0$

那么最大深度为$max(sum_{left}, max(sum_{left}), -min(sum_{right}))$

复杂度$O( n )$

Codeforces Round #604

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Beautiful String	√		8368
B. Beautiful Numbers	√		6432
C. Beautiful Regional Contest	√		4708
D. Beautiful Sequence	√	需要注意的是，尽管$cnt[min] < cnt[min+1]$，但$min$仍可能放在开头位置，样例"20000 39999 20000 0"	2331
E. Beautiful Mirrors	√	复习了一下概率dp和逆元~	1261
F. Beautiful Bracket Sequence (easy version)	X	没懂！！	134

E题题解

没什么好说的，概率dp

$cost_i = cost_{i-1} + 1 + (1-p_i)cost_i$

---

F题待完成！！！

Codeforces Round #607

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Suffix Three	√		8724
B. Azamon Web Services	√	找到可交换且字典序最小的字符a，若有多个a，取pos最大的那个 BTW：题解给出的代码挺巧妙的	3864
C. Cut and Paste	√	看了一眼题解，原来直接把前x个字符记录下来并保存到vector里也能过(935ms, $O(	S
D. Beingawesomeism	√	分类讨论	1115
E. Jeremy Bearimy	√	看题解！！！！	293
F. Miss Punyverse			30

Codeforces Round #608

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Suits	√		8738
B. Blocks	√		5835
C. Shawarma Tent	√		5611
D. Portals	√	做不到全局最优，只能局部最优+dp。题解说还可以维护一个undoable list当士兵不够的时候就undo，感觉可以用优先队列做	1168
E. Common Number	√	有点像二叉树，看题解吧	1538
F. Divide The Students	√	dfs剪枝	77

Educational Codeforces Round 78

题解 (opens new window)

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Shuffle Hashing	√		5820
B. A and B	√	[数学]看一波题解	3270
C. Berry Jam	√	比B简单	1996
D. Segment Tree	√	[优化]	514
E. Tests for problem D	√	[贪心]差分约束了半天出不了结果，还是看题解吧	291
F. Cards			73

Codeforces Round #609

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Equation	√		9859
B. Modulo Equality	√	这题用dict/map做，代码量会少一点	5103
C. Long Beautiful Integer	√	脑子没转过来，漏判一个条件~怎么回事??????	3471
D. Domino for Young	√	[思维]如果把图按棋盘的方式涂色，那么一个domino永远会占用一黑一白两种颜色的格子	1945
E. K Integers	√	看不懂题解。。估计是我境界不够	253

E题题解

题解讲的不是很清楚，这里做一下记录

首先，对于一个定值$k$，我们来讨论一下如何求解:

首先计算原序列中1 - k中的逆序对数为$inv$， 接下来我们改变一下原序列

arr = [1 if x <= k else 0 for x in arr]

这样任务就变成了计算产生$k$个连续的1所需的操作步数，显然只需要把所有数字移动到中位即可

那么对于$1 \le k \le n$，只需用一个树状数组维护逆序对和中位，并将$k$从1遍历到$n$即可求出答案。

（统计答案时可以用树状数组计算前缀和，因此代码中一共了两个树状数组）

Codeforces Round #610

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Temporarily unavailable	√		9204
B1. K for the Price of One (Easy Version)	√	[贪心]	6128
B2. K for the Price of One (Hard Version)	√	[贪心]	5059
C. Petya and Exam	√	[贪心]在$t_i - 1$时刻离开是最佳的	2532
D. Enchanted Artifact	√	[思维]关键在于如何求出a和b的数量	1255
E. The Cake Is a Lie			595

Educational Codeforces Round 79

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. New Year Garland	√		6821
B. Verse For Santa	√	**如果只能背到第x段，那么跳过大于x的段落是没用的！**不然就WA	4492
C. Stack of Presents	√		3687
D. Santa's Bot	√	除了A之外最简单的一题？	1672
E. New Year Permutations		感觉可以做，但是过题人数有点恐怖	32
F. New Year and Handle Change			36

Codeforces Round #630

两个号都上1600，再也不能打Div3了

题号	完成	备注	通过人数
A. Exercising Walk	赛时-AC		9009
B. Composite Coloring	赛时-AC	第11个质数:31,第12个:37	5767
C. K-Complete Word	赛时-AC		5066
D. Walk on Matrix	赛时-AC		3046
E. Height All the Same	AC		783
F. Independent Set			142
G. No Monotone Triples			11

E题题解

在完成分类讨论之后，这道题有两个入手点（已知$nm$为偶数）

1. $(O+E)^{mn}=\sum_{i=0}^{nm/2} C_{nm}^{2i}O^{2i}E^{nm-2i} + \sum_{i=1}^{nm/2}C_{nm}^{2i-1}O^{2i-1}E^{nm-2i+1}$

   $(O-E)^{mn}=\sum_{i=0}^{nm/2} C_{nm}^{2i}O^{2i}E^{nm-2i} - \sum_{i=1}^{nm/2}C_{nm}^{2i-1}O^{2i-1}E^{nm-2i+1}$

   两式相加除以2即为结果

2. 大神解法，目前还无法理解

   

3. 使用矩阵乘法：考虑$dp_{odd}[i]$代表$i$个格子中有奇数个奇数格的选法，$dp_{even}[i]$代表$i$个格子中有偶数个奇数格的选法，那么有

   $dp_{odd}[i] = dp_{odd}[i-1] \cdot E + dp_{even}[i-1] \cdot O$

   $dp_{even}[i] = dp_{even}[i-1] \cdot E + dp_{odd}[i-1] \cdot O$

   显然可以转化为矩阵乘法，矩阵快速幂可解！

   AC代码

Codeforces Round #635

改名叫Queueforces得了

题号	完成	备注	通过人数
A. Ichihime and Triangle	AC		17784
B. Kana and Dragon Quest game	AC		17336
C. Linova and Kingdom	题解AC(WA6)		7213
D. Xenia and Colorful Gems	题解AC		4646
E. Kaavi and Magic Spell	题解AC	Dp	641
F. Yui and Mahjong Set		交互题	46

D题AC代码 (opens new window)

---

E题：$dp[i][j]$表示已经使用了$i$个字符，得到的$A$仍需往头部添加$j$个字符才能构成前缀$T$时，有多少种可能

E题AC代码(题解我都写到注释里了) (opens new window)

Codeforces Round #637

题号	完成	备注	通过人数
A. Nastya and Rice	AC		16039
B. Nastya and Door	AC(3WA2/RE3)		11885
C. Nastya and Strange Generator	AC	有点麻烦，其实可以转化成求序列是否由数段连续上升序列组成	7929
D. Nastya and Scoreboard	题解AC		3195
E. Nastya and Unexpected Guest	题解AC	01BFS: 边权为0则放到队首，边权为1放到队尾	313
F. Nastya and Time Machine			57

D题题解：

一直想着用$dp[i][j]$来表示前$i$个数字操作了$j$次时能表示的最大数字，结果被复杂度被卡死在$O(2nklog_2k)=O(8e7)$(因为要排序并离散化)

题解给的是：$dp[i][j]$表示后$i$个数字操作了$j$次时是否合法($true$或$false$)，那么只要从$dp[n][k]$贪心的往前回溯即可得到最优解，复杂度$O(10nk)=O(4e7)$

PS: 4e7能过，说不定8e7也能过？

AC代码 (opens new window)，代码中$dp[i][j]$的含义与上述$dp$略微不同

---

E题题解：

如果在$T_i$到达了某个点$v$，令$T_i \equiv j \mod{G}$，那么对于任意时刻$T_j(T_j>T_i\ \&\ T_j\equiv T_i\mod G)$，都不应当到达该点$v$，否则发生循环（浪费时间）。因为$G\le 1000$，我们让每个点对应$G$个新图上的点$V_{ij}$，跑01BFS即可。

AC代码 (opens new window)，代码中有01dfs的解析

另：大佬的另一种思路

大佬的AC代码 (opens new window)

Educational Codeforces Round 86

题号	完成	备注	通过人数
A. Road To Zero	AC(3WA2/1WA1)	1. inf不够大 2. 没看到x,y>0	12855
B. Binary Period	AC		11321
C. Yet Another Counting Problem	题解AC		3934
D. Multiple Testcases	题解AC		1676
E. Placing Rooks	题解AC	容斥	313
F. Make It Ascending			19

C题题解:

$(ab+x)\mod a \mod b=x\mod a\mod b$，且$(ab+x)\mod b \mod a=x\mod b\mod a$

可以看出循环节大小为$ab$

AC代码 (opens new window)

---

D题题解：

设$cnt_i$为大于等于$i$的数组个数，那么所需的最小testcase数为$ans=max(\lceil \frac{cnt_i}{c_i} \rceil)$。

接着把$m$从小到大/从大到小排序，第$i$个数装进第$i\mod ans$个testcase中。

AC代码 (opens new window)

---

E题题解：

由于只有$n$块石头，因而可以每行（或每列）有且只有一块石头，考虑每行一块的情况，结果乘2（除非k=0，此时每行与每列都满足"有且只有一块石头"）即可。

由观察可发现，问题可转化为：把$n$块石头，分到$n-k$列，使得每列至少有一块，共有多少种分法。

首先任选$n-k$列，有$C_n^{n-k}$种选法，下面考虑如何把$n$块石头分到$c$列中

根据容斥原理，首先每块石头有$c$种选择（不同行的石头不等价），即$c^n$，减去单列为空的情况$C_c^1(c-1)^n$，补上两列为空的$C_c^2(c-2)^n$，再减去三列为空的$C_c^3(c-3)^n$，以此类推，得到公式$ans=\sum_{i=0}^c(-1)^iC_c^i(c-i)^n$

AC代码 (opens new window)

PS：容斥原理：$\mid\large\cup_{i=1}^nA_i\mid=\sum_{C\subseteq B}(-1)^{size(C)-1}\mid\large\cap_{e\in C}e\mid$

PS2: 事实上，上述的$ans$即为第二类斯特林数$S(n, c)$乘上$c!$（因为不同的行之间不等价）

Codeforces Round #647

题号	完成	备注	通过人数
A. Johnny and Ancient Computer	AC(WA2)		13351
B. Johnny and His Hobbies	AC(2WA2)		10803
C. Johnny and Another Rating Drop	AC		9480
D. Johnny and Contribution	AC		3695
E. Johnny and Grandmaster	题解	很棒的题解 (opens new window)（与出题者思路不同）	687
F. Johnny and Megan's Necklace			59

Codeforces Round #648

心态炸了，A题这么简单都没过，不知得掉多少分

UPD:1631$\to$1630

题号	完成	备注	通过人数
A. Matrix Game	赛后AC(4WA2)	一开始看错了题，然而后来还是没过...	13357
B. Trouble Sort	AC		11706
C. Rotation Matching	AC		10021
D. Solve The Maze	赛后AC(2WA7)	一个变量名写错了，愣是没检查出来（居然Wa7，我也是服了）	6152
E. Maximum Subsequence Value	AC(2WA6,WA3)	没有仔细分析：子序列的元素个数不会超过3（离比赛结束还有30s的时候才AC）	3837
F. Swaps Again	题解AC(WA119)		1946
G. Secure Password	题解AC	很有意思的解法	211

---

If we consider the unordered pair of elements $\{ai,an−i+1\}$, then after any operation, the multiset of these pairs (irrespective of the ordering of elements within the pair) stays the same!

F题AC代码 (opens new window)

关键在于找到通过B构造出A的方法。

---

相关知识: Sperner's theorem

E题通过编码方式，使得任意两个编码互不为子集，进而查询时只需查询该位为1的OR。

E题AC代码(看标程前) (opens new window)

E题AC代码(看标程后) (opens new window)

Codeforces Round #646

题号	完成	备注	通过人数
A. Odd Selection	AC(WA3)	能够暴力$O(n)$，绝不优化到$O(1)$	16056
B. Subsequence Hate	AC(WA2)		11592
C. Game On Leaves	AC		9145
D. Guess The Maximums	AC(3WA7)	存在$\cup S_i\not=A$的情况！！	2519
E. Tree Shuffling	AC		3769
F. Rotating Substrings		DP？没懂	525

---

B题AC代码 (opens new window)

---

Educational Codeforces Round 88

题号	完成	备注	通过人数
A. Berland Poker	AC		12854
B. New Theatre Square	AC		10248
C. Mixing Water	题解AC	算出k的最优值(double)	3275
D. Yet Another Yet Another Task	AC(WA5)		1426
E. Modular Stability	题解AC		1289
F. RC Kaboom Show			24

---

C题AC代码 (opens new window)

---

D题AC代码 (opens new window) 总感觉是我想复杂了，做法：设第$i$个数为区间最大值，RMQ取左侧前缀和最小，右侧前缀和最大值。

D题题解做法 (opens new window) 很短，使用前缀和求最大子区间和（非双指针）。 感觉智商受到了侮辱

另外，设$dp[i]$为以$i$结尾的最大子区间和，那么$dp[i]=max(val[i],val[i]+dp[i-1])$，即要么自己单独成为一个子区间，要么与$i-1$的最优解结合。

---

E题AC代码 (opens new window)

互换顺序而对任意$x$都不影响结果，那么$\forall i,a_i\mid a_j(a_j=\min\limits_{i}\ a_i)$

Educational Codeforces Round 89

题号	完成	备注	通过人数
A. Shovels and Swords	AC		9163
B. Shuffle	AC		7698
C. Palindromic Paths	AC		4708
D. Two Divisors	看代码AC		1358
E. Two Arrays	看代码AC		679
F. Jog Around The Graph			42
G. Construct the String			25

---

D题AC代码 (opens new window) 特殊构造

$a=p_0^{x1}p_1^{x2}p_2^{x3}...p_n^{xn},gcd(a,\frac{a}{p_i^{xi}} + p_i)=1$

---

想了半天Dp做法，看了别人代码之后才发现我看漏了个条件：$b_i$为升序

E题AC代码 (opens new window)

---

Codeforces Round #645

题号	完成	备注	通过人数
A. Park Lighting	AC		20013
B. Maria Breaks the Self-isolation	AC		16465
C. Celex Update	题解AC	从最小一步一步转移到最大的情况	10574
D. The Best Vacation	题解AC		5404
E. Are You Fired?	题解AC	转化为前缀和	1302
F. Tasty Cookie			280

---

We will find such an optimal segment that its end coincides with the end of some month.

D题AC代码 (opens new window)

---

E题AC代码 (opens new window)

如果暴力地对每一个$k$验证一遍，复杂度$O(n^2)$，显然超时。

观察到暴力的过程中有许多重复计算，因此考虑将问题转化。对于本题，可以将其转化为前缀和。

另一种与题解相似，但更容易想到的方法。

---

Codeforces Round #649

题号	完成	备注	通过人数
A. XXXXX	AC		10493
B. Most socially-distanced subsequence	AC	比A简单	8885
C. Ehab and Prefix MEXs	AC		5510
D. Ehab's Last Corollary	2WA12,2WA21,看代码AC		1514
E. X-OR	题解AC	题解的三种做法都是随机	279

---

D题AC代码 (opens new window) 一种与题解思路相通，但更为巧妙的做法（Um_nik的做法）

另外，如果采用了dfs的方法，又发现图有环，且所有环的大小都大于$k$，就可以放心的在任意一个$depth[v] \ge k$的点跳$fa[v]$。没有环就更简单了~

---

E题随机做法1 (opens new window)

E题随机做法2 (opens new window)

Educational Codeforces Round 87

题号	完成	备注	通过人数
A. Alarm Clock	AC		11520
B. Ternary String	AC		9155
C1. Simple Polygon Embedding	AC		6609
C2. Not So Simple Polygon Embedding	半题解AC		1402
D. Multiset	AC		1510
E. Graph Coloring	题解AC	二分图	357
F. Summoning Minions			75
G. Find a Gift			22

---

C2AC代码 (opens new window)

---

D题树状数组 (opens new window) $O(nlog^2n),826ms$

We can do it with binary search as follows: let's write a function that, for a given element x, tells the number of elements not greater than x in the resulting multiset.

D题技巧 (opens new window) $O(nlogn),389ms$

---

E题AC代码 (opens new window)

Codeforces Round #651

BestRatingChanges (opens new window) Wow

$Rating\to1782(+152)$

题号	完成	备注	通过人数
A. Maximum GCD	AC		15305
B. GCD Compression	AC		11243
C. Number Game	AC(WA3)	$sqrt(n)$质数分解的时候忘了$+1\quad if(n>1)$	8730
D. Odd-Even Subsequence	AC(3WA10)	边界没控制好	2346
E. Binary Subsequence Rotation	AC(WA8)		1412
F1. The Hidden Pair (Easy Version)	题解AC		334
F2. The Hidden Pair (Hard Version)			223

F1AC代码 (opens new window)

---

F2题解：同F1一样先找到对应的根$root$，设$depth[root]=0$，接着有一个结论：$s,f$至少一个的$depth<\lfloor\frac{n}{2}\rfloor$，又因为如果$s\ne root,f\ne root$，则$s,f$分别在$root$下的不同子树中，因此二者至少一个所在的子树深度不超过$\lfloor\frac{n}{2}\rfloor$

Codeforces Round #643

这套题比较简单

题号	完成	备注	通过人数
A. Sequence with Digits	AC		15097
B. Young Explorers	AC		13845
C. Count Triangles	AC		6488
D. Game With Array	AC		10549
E. Restorer Distance	AC		2696
F. Guess Divisors Count		数学大题	424

---

C题AC代码 (opens new window)

C题前缀和做法 (opens new window)

---

E题的三分法 (opens new window)

ll twoPointBinSearch(ll l, ll r, function<ll(ll)>cost){
    while(l < r){
        ll mid = (l + r) >> 1;
        ll mmid = (mid + r + 1) >> 1;
        ll cost_m = cost(mid), cost_mm = cost(mmid);
        if(cost_m >= cost_mm){ // 下凸包
            l = mid + 1;
        }else{
            r = mmid - 1;
        }
    }
    return l;
}

注意$mid$与$mmid$的取法

Codeforces Round #641

题号	完成	备注	通过人数
A. Orac and Factors	AC		16546
B. Orac and Models	AC	第一次在前两题遇到Dp	10753
C. Orac and LCM	题解AC	想了半天怎么求$gcd(\{a_k\mid k\ne i\})$	6560
D. Orac and Medians			2975
E. Orac and Game of Life			1145
F. Slime and Sequences (Easy Version)			20

Codeforces Round #652

$Rating\to 1800(+18)$

题号	完成	备注	通过人数
A. FashionabLee	AC		15561
B. AccurateLee	AC		11159
C. RationalLee	AC(RE3)	没改maxn，检查了半天	7934
D. TediousLee	AC		3307
E. DeadLee	题解AC	贪心	534
F. BareLee			116

---

E题AC代码(python) (opens new window) (预分配空间能够省一些时间(~100ms))

Codeforces Round #654

题号	完成	备注	通过人数
A. Magical Sticks	AC		16414
B. Magical Calendar	AC		11076
C. A Cookie for You	3WA3, 题解AC	一个简单地贪心题，怎么比E2还难...	9737
D. Grid-00100	AC		6104
E1. Asterism (Easy Version)	AC		2290
E2. Asterism (Hard Version)	2TLE5, AC	TLE两次，发现是maxn不够大	857
F. Raging Thunder	理论AC	线段树合并，细节之多跟模拟题有的一拼	99

Codeforces Round #655

题号	完成	备注	通过人数
A. Omkar and Completion	AC		18453
B. Omkar and Last Class of Math	题解AC		13071
C. Omkar and Baseball	看数据AC	坑	9198
D. Omkar and Circle	AC	比BC简单？	2994
E. Omkar and Last Floor	题解AC	dp	356
F. Omkar and Modes			145

Codeforces Round #685

题号	完成	备注	通过人数
A. Subtract or Divide	题解AC		14018
B. Non-Substring Subsequence	AC		11329
C. String Equality	AC		7362
D. Circle Game	AC		5100
E1. Bitwise Queries (Easy Version)	题解AC	$a+b=a\oplus b+(a\& b)*2$	2151
E2. Bitwise Queries (Hard Version)	题解AC	$a\oplus b$为某位$1$，即该位$a,b$不同	1314
F. Nullify The Matrix	题解AC	awsome	335

Educational Codeforces Round 98

题号	完成	备注	通过人数
A. Robot Program	AC		10628
B. Toy Blocks	题解AC	不用管具体怎么放，只看总数即可	3897
C. Two Brackets	AC		9127
D. Radio Towers	AC(50min)		2594
E. Two Editorials	题解AC		168

Codeforces Round #684

题号	完成	备注	通过人数
A. Buy the String	AC		13230
B. Sum of Medians	AC		10657
C1. Binary Table (Easy Version)	看代码AC	很考验代码技巧	4792
C2. Binary Table (Hard Version)	看代码AC		2041
D. Graph Subset Problem	题解AC	无向图的“拓扑序”	163
E. Greedy Shopping	题解AC	痛苦面具	310

Codeforces Round #683

题号	完成	备注	通过人数
A. Add Candies	AC		9900
B. Numbers Box	AC		8514
C. Knapsack	AC		6230
D. Catching Cheaters	AC	痛苦Dp，用了50分钟才AC。结果发现题解的Dp思路更简单，是我想得太复杂	2589
E. Xor Tree	题解AC	一看就懂，一做就懵	660

Codeforces Round #687

题号	完成	备注	通过人数
A. Prison Break	AC		8688
B. Repainting Street	AC		6572
C. Bouncing Ball	AC		4110
D. XOR-gun	看数据AC		1524
E. New Game Plus!	题解AC		512

Educational Codeforces Round 99

题号	完成	备注	通过人数
A. Strange Functions	AC		12293
B. Jumps	AC		6941
C. Ping-pong	AC		7952
D. Sequence and Swaps	AC		3049

Codeforces Round #688

题号	完成	备注	通过人数
D. CheckPoints	AC		2796
E. Dog Snacks	题解AC		1182
F. Even Harder	AC	Dp，比E简单...	348

Codeforces Round #689

题号	完成	备注	通过人数
E. Water Level	题解AC		1388
F. Mathematical Expression	题解		269

Educational Codeforces Round 100

题号	完成	备注	通过人数
C. Busy Robot	AC		1667
D. Pairs	AC		1007

Codeforces Round #691 (Div. 2)

题号	完成	备注	通过人数
C. Row GCD	题解AC		5698
D. Glass Half Spilled	题解AC	double数组初始化为负无穷：memset(0xfe)	835

Codeforces Round #692

题号	完成	备注	通过人数
C. Peaceful Rooks	AC		3140
D. Grime Zoo	题解AC		763

Educational Codeforces Round 101

题号	完成	备注	通过人数
C. Building a Fence	AC		3470
D. Ceil Divisions	AC		2360
E. A Bit Similar	题解AC		236

Codeforces Round #694 (Div. 2)

题号	完成	备注	通过人数
D. Strange Definition	AC	忘了ll，debug了好久	2639
E. Strange Shuffle			251
F. Strange Housing	题解AC	题意表述不清晰	929

Codeforces Round #695 (Div. 2)

题号	完成	备注	通过人数
D. Sum of Paths	题解AC		2407
E. Distinctive Roots in a Tree			750

Div. 3

Codeforces Round #587

我的AC代码(C/E2/F) (opens new window)

题号	完成	一句话题解	通过人数
A. Prefixes	√	Water	5931
B. Shooting	√		5577
C. White Sheet	√	有点小麻烦	1331
D. Swords	√		3388
E1. Numerical Sequence (easy version)	√		670
E2. Numerical Sequence (hard version)	√	不容易啊	128
F. Wi-Fi	√	DP好难	185

Codeforces Round #590

我的AC代码(B2/D/E/F) (opens new window)

题号	完成	一句话题解	通过人数
A. Equalize Prices Again	√		8366
B1. Social Network (easy version)	√		6851
B2. Social Network (hard version)	√	我服了，出题人专门出了一组数据来Hack unordered_set，用set即或自定义hash (opens new window)	4712
C. Pipes	√		2924
D. Distinct Characters Queries	√	看题解半天都看不懂，才发现是读错题了	2035
E. Special Permutations	√		455
F. Yet Another Substring Reverse	√	感觉这题比F简单，刚开始还以为是水过的（毕竟DFS），后来发现只要把DFS改成一个for就是正解了	151

Codeforces Round #595

我的AC代码(F题) (opens new window)

题号	完成	一句话题解	通过人数
A. Yet Another Dividing into Teams	√		8354
B1. Books Exchange (easy version)	√		7001
B2. Books Exchange (hard version)	√		4520
C1. Good Numbers (easy version)	√		4500
C2. Good Numbers (hard version)	√		2785
D1. Too Many Segments (easy version)	√		893
D2. Too Many Segments (hard version)	√		726
E. By Elevator or Stairs?	√		1483
F. Maximum Weight Subset	√	[树Dp] dp[u][dep]代表以u为根的子树中，被选取的点深度至少为dep时最大的weight之和	152

Codeforces Round #598

我的AC代码（C/D/E/F） (opens new window)

题号	完成	一句话题解	通过人数
A. Payment Without Change	√		7365
B. Minimize the Permutation	√	看到$n \le 100$且$t \le 100$就该想直接想到暴力(优化成$O(n)$的意义不大)	3716
C. Platforms Jumping	√	贪心 + 实现	1320
D. Binary String Minimizing	√	贪心	2583
E. Yet Another Division Into Teams	√	一道带标记的Dp(Ps. 要是能注意到最优解中一个队伍不会超过5人，这题就更好做了(见题解))	392
F. Equalizing Two Strings	√	让B变成A，不如让AB都变成有序的串(详见代码)	322

F题题解

当字符串s没有重复出现的字符时

every swap of two adjacent elements changes the parity of the number of inversions

Codeforces Round #605

我的AC代码 (opens new window)

题号	完成	备注	通过人数
A. Three Friends	√		6972
B. Snow Walking Robot	√		4486
C. Yet Another Broken Keyboard	√		5061
D. Remove One Element	√		2429
E. Nearest Opposite Parity	√	图论，痛哭涕流，看题解吧	594
F. Two Bracket Sequences	√	看了题解，是个三维Dp	188

F题题解

设dp[i][j][k]代表字符串ans的最小长度，其中s[:i]和t[:j]为ans的子序列，且ans中( - )的数量为k，可知如果k小于0，该字符串一定不合法，故有$0 \le k \le max(len(s), len(t))$

则可按如下规则更新dp

dp[i+1][j][k+1] = dp[i][j][k] + 1 if s[i] == '('

dp[i][j+1][k+1] = dp[i][j][k] + 1 if t[j] == '('

dp[i+1][j+1][k+1] = dp[i][j][k] + 1 if s[i] == t[j] == '('

dp[i+1][j][k-1] = dp[i][j][k] + 1 if s[i] == ')'

dp[i][j+1][k-1] = dp[i][j][k] + 1 if t[j] == ')'

dp[i+1][j+1][k-1] = dp[i][j][k] + 1 if s[i] == t[j] == ')'

同时根据定义，有

dp[i][j][k] = min(self, dp[i][j][k+1] + 1, dp[i][j][k-1] + 1)

则dp[len(s)][len(t)][0]为答案

按dp路径回溯即可得到ans

Codeforces Round #611

题解 (opens new window)

题号	完成	备注	通过人数
A. Minutes Before the New Year			8731
B. Candies Division			6998
C. Friends and Gifts			2437
D. Christmas Trees			1097
E. New Year Parties			973
F. DIY Garland			177

Codeforces Round #627

第一次AK，用了70分钟，就不记录了吧~

UPD: 打一场Rating就上1700+，我傻了

Codeforces Round #629

才过了4题，居然还能涨Rating...

题号	完成	备注	通过人数
A. Divisibility Problem	赛时-AC		17088
B. K-th Beautiful String	赛时-AC		9001
C. Ternary XOR	赛时-AC		9944
D. Carousel	赛时-AC		2266
E. Tree Queries	赛时-TLE AC		977
F. Make k Equal	理论AC	要让(排序后的)左边出现$n$个$m$，首先让左边的数字全变为$m-1$，然后结果$+n$即可	368

E题题解

对于判断节点$u$是否在节点$v$到$root$的路径上

有一个巧妙的方法

void dfs(int v, int par = -1) {
    tin[v] = T++;
    for (auto to : g[v]) {
        if (to == par) continue;
        dfs(to, v);
    }
    tout[v] = T++;
}

对于$u$的子树上任意节点$v\ (v\ne u)$，有$tin[u]<tin[v]<tout[v]<tout[u]$

Codeforces Round #644

题号	完成	备注	通过人数
A. Minimal Square	AC		14736
B. Honest Coach	AC		14749
C. Similar Pairs	AC		11532
D. Buying Shovels	AC		8368
E. Polygon	AC		8155
F. Spy-string	AC		2585
G. A/B Matrix	AC		1200
H. Binary Median	题解	考虑左边有多少个数字，一直奔着那个方向去就行	798